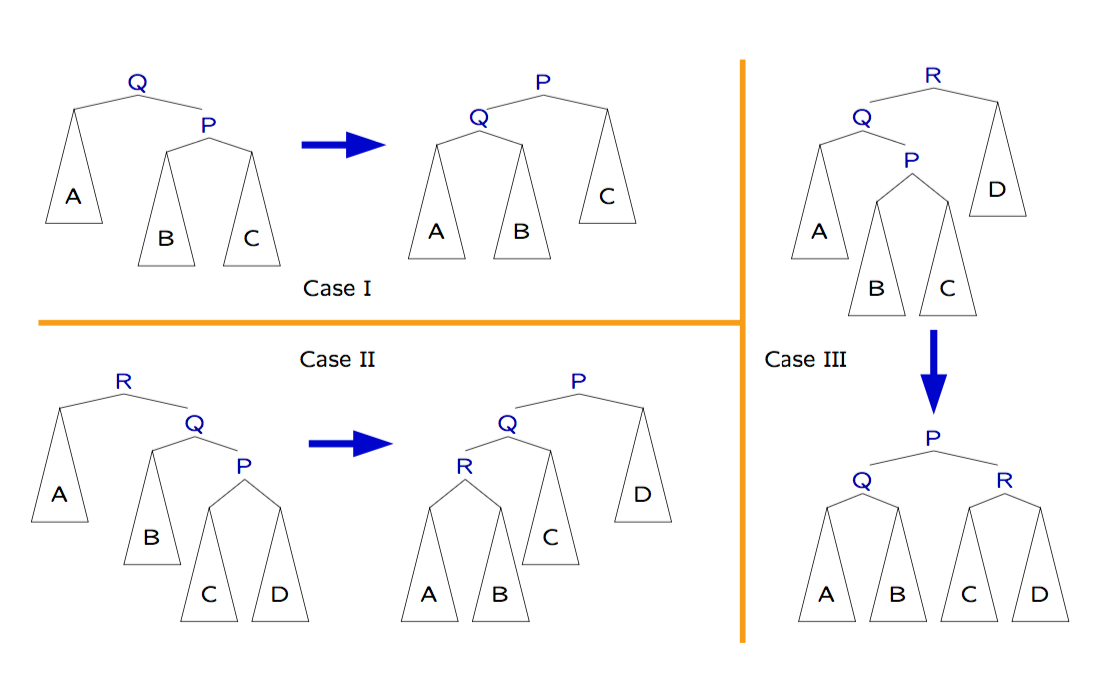
Tree Rotation

A rotation involves a pair of nodes x and its parent y.
After the rotation x is the parent of y. The update is done in such a way as to guarantee that the in-order traversal of the tree does not change.
A left rotation is the mirror image variant of right rotation

Splay Trees (self-adjusting search trees)

Every time a node is accessed in a splay tree, it is moved to the root of the tree. We will show that the amortized cost of the operation is O(logn).
Splay trees perform movements in a very special way that guarantees this logarithmic amortized bound.
- Apply rules to 3-node tree defined by x, x’s parent (y), and x’s grandparent (z), until x is at the root of the tree.

Zig, Zig-Zag, Zig-Zig

Rotation number: Zig(1), Zig-Zag(2), Zig-Zig(2)
A splay step refers to applying one of these rewrite rules.
Each such step can be executed in constant time.
Each rule has a mirror image variant
The Zig-zig rule is the one that distinguishes splaying from just rotating x to the root of the tree. <!-- ``` zig:
```
  y        x
 /    =>    \
x            y
```
```
y            x
 \    =>    /
  x        y
```
zig-zag:
```
z          z          x
```
/ / / \ y => x => y z \ /
```
x      y
```
z z x \ \ / \
```
y  =>   x    =>    z   y
```
/ \ x y zig-zig: z y x
/ * / \ \ y => x z => y / \ x z

z y x \ * / \ => / y => z x y \ / x z ``` -->

Analysis

Notations:

Any tree $T$
- $s(x) = \sum_{x \in T(x)}w(x)$
  - The size of a node $x$ in $T$ is the total weight of all the nodes in the subtree rooted at $x$,
- $r(x) = \lfloor \lg s(x) \rfloor$
  - The rank of a node $x$
- $\Phi (T) = \sum_{x \in T} r(x)$
  - Potential function corresponding to the tree $T$

Observations:

Doing a rotation between a pair of nodes $x$ and $y$ only effects the ranks of the nodes $x$ and $y$, and no other nodes in the tree.
Furthermore, if $y$ was $x$’s parent before the rotation, then the rank of $y$ before the rotation equals the rank of $x$ after the rotation.
In the banker’s view of amortized analysis, we can think of having $r(x)$ tokens on node $x$.

Amortized Logic:

if we can bound the amortized cost of each of the operations, and the final potential is at least as large as the initial potential, then the bound we obtained for the amortized cost applies to the actual cost.

Whenever you do a amortized analysis, it needs to be respect certain potential function, otherwise it is not even defined

Access Lemma:

The amortized cost respect to the potential function $\Phi (T) = \sum_{x \in T} r(x)$ is bounded by $\leq 3(r(t) - r(x)) + 1$

this is amortized bound for individual splay operations
Instead of a constant bound, it is related to the rank of nodes you access with.
$3(r(t) - r(x)) + 1 = 3( \log n - r(x)) + 1 \leq 3(\log n) + 1 \rightarrow$ amortized cost is $O(\log n)$

Balance Theorem:

A sequence of $m$ splays in a tree of $n$ nodes takes time $O(m\log n+n\log n)$.

Static Optimality Theorem

Let $T$ be any static search tree with $n$ nodes. Let $t$ be the number of comparisons done when searching for all the nodes in a sequence $s$ of accesses. (This sum of the depths of all the nodes). The cost of splaying that sequence of requests, starting with any initial splay tree is $O(n^2 + t)$.

splay trees perform within a constant factor of any static tree.

Static Finger Theorem

Consider a sequence of $m$ accesses in an $n$-node splay tree. Let $a[j]$ denote the $j$-th element accessed. Let $f$ be a specific element called the finger. Let $|e - f|$ denote the distance (in the in-order list of the tree) between elements $e$ and $f$. Then the following is a bound on the cost of splaying the sequence:

if the accesses have spatial locality (they cluster around a spacific place) then the sequence is cheap to process.
if we measure the cost of an access by the log of the distance to a specific element called the finger, then this is a bound on the actual cost: $O(m+n\log n+ \sum_{1 \leq j \leq m} \log (|f - a[j]| + 1))$

Working Set Theorem

In a sequence of $m$ accesses in an $n$-node splay tree, consider the $j$-th access, which is to an item $x$. Let $t(j)$ be the number of different items accessed between the current access to $x$ and the previous one. (If there is no previous access, then $t(j) = n$ the size of the tree.) Then the total cost of the access sequence is $O(m+n \log n+ \sum_{1 \leq j \leq m} \log (t(j)+1)$

If I access an element, then shortly after this, I access it again, then the second access is cheap.

5. Splay Tree Analysis