Knuth–Morris–Pratt algorithm

• Notes from KMT wiki

KMP algorithm searches for occurrences of a "word" W within a main "text string" S by employing the observation that when a mismatch occurs, the word itself embodies sufficient information to determine where the next match could begin, thus bypassing re-examination of previously matched characters.

• Supposed W with size $$n$$ and S with size $$k$$.

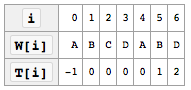
• We can build up a table T with $$O(k)$$ for $$O(1)$$ look up in the KMP algorithm, the table record the "sufficient information" embodied in the word itself.

• Assuming the prior existence of the table T, the search portion of the KMT algorithm has complexity $$O(n)$$.

Table T Intuition

W = "ABCDABD" and S = "ABC ABCDAB ABCDABCDABDE"

m, denoting the position within S where the prospective match for W begins,

i, denoting the index of the currently considered character in W.

In each step the algorithm compares S[m+i] with W[i] and advances i if they are equal.

after this pic: m = 3, i = 0

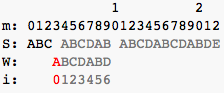after this pic: m = 4, i = 0

after this pic: m = 10 - 2, i = 2

after this pic: m = 10, i = 0

after this pic: m = 11, i = 0

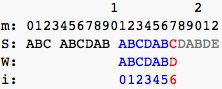after this pic: m = 17 - 2, i = 2

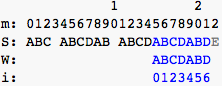after this pic: find a match!

• The entries of T are constructed so that **if we have a match starting at S[m] that fails when comparing S[m + i] to W[i], then the next possible match will start at index m + i - T[i] in S.

• T[i] is the amount of "backtracking" we need to do after a mismatch.

• T[0] = -1, which indicates that if W[0] is a mismatch, we cannot backtrack and must simply check the next character

• Although the next possible match will begin at index m + i - T[i], we need not actually check any of the T[i] characters after that, so that we continue searching from W[T[i]]